Research

On this page, I would like to present the results of my nearly 6 year work and research at the Centre for biomedical image analysis (CBIA) at the Faculty of Informatics, Masaryk University in Brno. CBIA is an interdisciplinary group consisting of scientists with experience in biology, medicine, physics, computer science and mathematics. Its specialization is the acquisition of 2D and 3D images of cells and sub-cellular structures using modern fluorescence microscopes and their subsequent analysis. The primary goal of these observations are the efforts to understand the organization and function of biological material in human cells and clinical applications focusing on early diagnosis, prevention and treatment of malignant diseases.
Software
As an employee I have contributed significantly to the following software packages:
- Acquiarium (screenshots) – Software for automated acquisition of large amounts of 2D and 3D data using fluorescence microscopes and their subsequent batch processing and analysis (correction of optical aberrations, segmentation, colocalization, statistics, etc.). It is a cross-platform application written in C++ using the wxWidgets toolkit. Personally, I have been deeply involved particularly in the development of the data display and evaluation part of the software (e.g., I have implemented a dynamic plug-in system for the application).
- v3dlib – A cross-platform library written in C++ using the wxWidgets toolkit. Its main purpose is the visualization of 2D and 3D from optical microscopes.
- i3dlib – A cross-platform library written in C++ consisting of a large collection of basic as well as advanced image processing algorithms.
Research activities

During my postgraduate study I was interested in the development of fast and realiable image processing algorithms for evaluation of 2D and 3D data from fluorescence microscopes. In particular, the main topic of my research was image segmentation, i.e., the detection of objects (in this case, cells and cell nuclei) and their boundaries in given image data. Ideally, a segmentation approach should be fully automatic, accurate and sufficiently fast in order to enable reliable and unsupervised processing of large amounts of data. However, due to the low quality of the images, these objectives are only hardly achieved in practice. I was engaged into a long-term project “Marker determination, screening and early diagnostics of cancer diseases using highly automated processing of multidimensional biomedical images” by the Ministry of Education of the Czech Republic. Furthermore, I have also extensively collaborated with the research centre Centro de investigación médica aplicada (CIMA) at Universidad de Navarra in Pamplona, Spain, where I spent two quarterly stages in 2008 and 2010.
Ph.D. thesis and publications
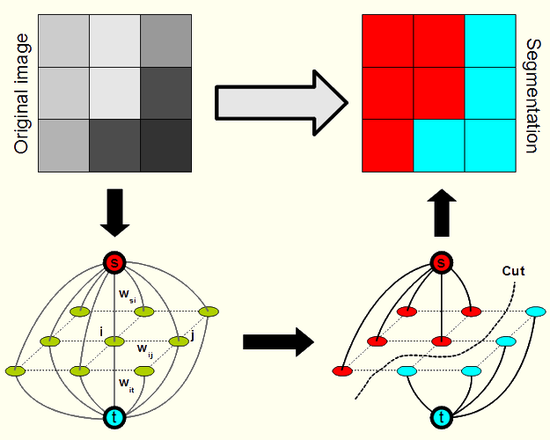
In my research, I was dealing with so-called energy minimization approaches to image segmentation. In such methods, the optimum segmentation is defined as a minimum of a suitable energy function. Various traditional mathematical techniques may be exploited to determine the minimum. In my case, the methods were based on combinatorial optimization, more concretely, on finding a minimum cut in a specifically designed graph. This approach was first proposed in the work of Y. Boykova (see a list of his scientific publications mostly on this topic) and his colleagues. The results of my research (see below) are available in my Ph.D. thesis, a freely distributable open source library and in publications presented in journals and on international conferences:
Illustration of the principles of the method:
Graph cut library
The implementation of most of the algorithms developed and described in the Ph.D. thesis is available in the following library. It is written in C++ and freely distributed under the GPL license.
- The home page of the library on the CBIA web with examples of usage
- Documentation
- Download: library source code (ZIP), MATLAB interface (ZIP)
Results
The key results introduced in the thesis are summarized and illustrated in this section.
Metric approximation
Commonly employed energy functions often comprise a boundary length dependent term (we seek the segmentation with a short, i.e., smooth, boundary). Thus, it is necessary to embed an Euclidean or Riemannian metric approximation into the graph. For fluorescency microscopy data this approximation has to cope with anisotropic resolution (i.e., not the same in all axes) of the images. Moreover, an approximation with a smaller error was devised in the thesis.
Riemannian metric approximation for neighbourhoods of various size (N4, N8, N6 a N32):




Catenoid reconstruction for neighbourhoods of various size (N26, N98) and a comparison against a continuous method:
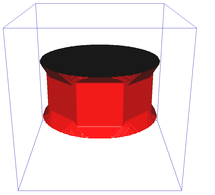
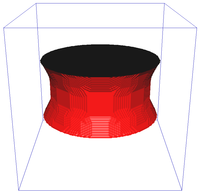
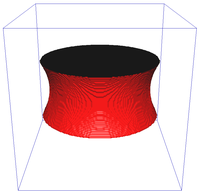
Image segmentation
We have proposed two segmentation algorithms for cells and cell nuclei that exploit the aforementioned metric approximation. The first one is a modification of the popular Chan-Vese segmentation model with a robust initialization, improved boundary smoothness and low memory footprint:
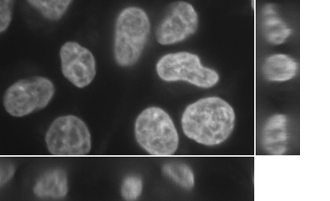

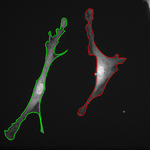
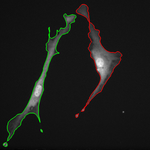
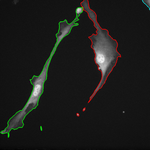
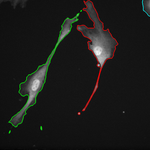
The method can be extended to a multi-phase (in the image below there are 3 levels – the background, cytoplasm and the nuclei) segmentation approach:
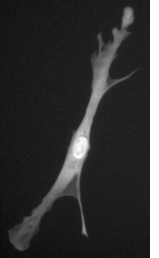
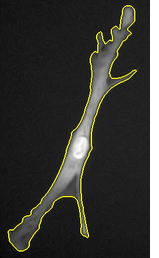
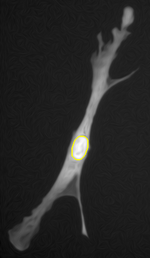

The second algorithm is based on the geodesic segmentation model and it is intended for separation of dense clusters of touching cell nuclei:
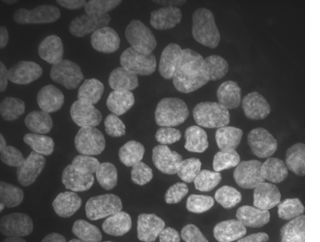
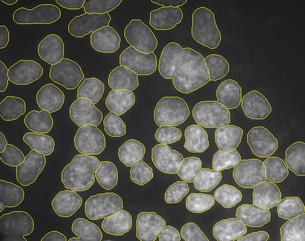
Topology preserving and cell tracking
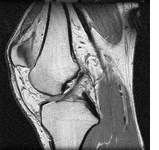
In the final part of the thesis, the graph cut based segmentation algorithms are integrated with topology preserving priors enabling us to define the number of objects being sought and their topology in advance. An example is presented here where two marked bones are extracted from an MRI image of a knee:
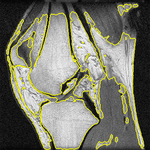
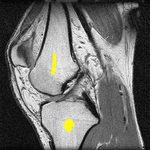
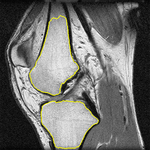
The topological priors can be combined with the Chan-Vese model in order to develop a fast motion tracking method for cells in time-lapse series where the individual objects are allowed to touch or split into multiple parts: